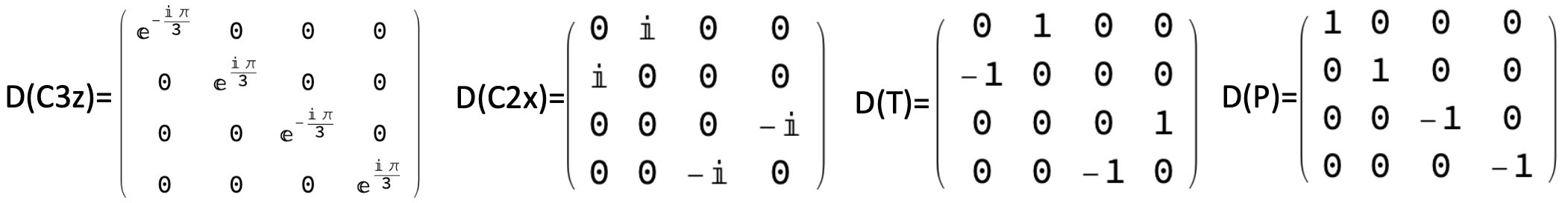The g-factor calculation

Requirements:

1. Read the Chapter 2 of [Winkler-2003-Spin-orbit coupling effects in two-dimensional electrons and hole systems], [arXiv:1512.05084] and [PRB 82, 045122 (2010)] to acquire the theoretical background about the kp Hamiltonian and g-factors.
2. Know the basic procedures of VASP.
3. Theory of invariants.(Group theory)

Procedures:

1. Perform a static self consistent calculation to get files “CHG” and “CHGCAR”.
2. Take the band calculation at a single $k$ point to get the files “WAVECAR” and “EIGENVAL”(saved as “EIGENVAL.Pi”)
3. Calculate the momentum matrix elements with [vasp.5.3.song.2018]
4. Extract the kp Hamiltonian and the g-factor with matlab [demo.m].

Demo—Bi2Te3:

Get the demo file here.

How to run this demo:

1. On your sever: qsub demo.pbs
   Before doing this, you have to change the variable “vasp_song” in file “demo.pbs” to your path of [vasp.5.3.song.2018]. The procedures 1, 2 and 3 has been included in this pbs file.
2. On your local computer with matlab:
   scp "Delta:~/demo/{POSCAR,EIGENVAL.Pi,MAT*.m}" ./demo/data
3. run demo.m in matlab.

How to understand this demo:

1. The kp Hamiltonian and gfactor of Bi2Se3 family with up to third order of $k$ is summarized in [arXiv:2203.14301] section “Sb2Te3 thin film” which explains that what these parameters represent.

Key points:

1. Due to the degeneracy, the symmetry representation has to be fixed by hand in demo.m. In Bi2Se3 family we fix the representation as

   

   The raw representation is saved in variable “C3z”, “C2x”, “T” and “P”. The transformed representation is saved in “C3z_trans”, “C2x_trans”, “T_trans” and “P_trans”. Procedures to fix the representation is explained in the Appendix PPT. Under this representation the table of theory of invariants is

   

   From which we can construct the analytical expression of kp Hamiltonian and g-factors as given in [arXiv:2203.14301] section “Sb2Te3 thin film”.

2. Band Indices, on which construct the kp Hamiltonian, has to be declared at “band_start” and “band_end” in demo.m, also at “bstart” and “bend” in INCAR.song.#

Appendix: